User Guide¶

TL;DR These are notes and highlights. For usage see the Workflow Outline, Examples Gallery, and API

fitgrid.Epochs¶

Fitting linear regression models in Python and R with formulas like y ~ a + b + a:b in Python (patsy, statsmodels.formula.api) or R (lm, lme4::lmer) assumes the data are represented as a 2D array with the variables in named columns, y, a, b and values (“observations”, “scores”) in rows.

fitgrid follows this format with the additional assumption that the data are vertically stacked fixed-length time-series “epochs”, so the user must specify two additional columns of values that together uniquely identify the epoch and time of the data row.

Format¶

Specification: Data for fitgrid modeling should be prepared as a single pandas.Dataframe with these columns and data types:

epoch_id: integer
time: integer
a set of channel data columns: numeric
a set of predictor variable columns: numeric, string, boolean

Each epoch must have a unique integer identifier in the epoch_id column. Gaps are OK, duplicates are not.

The integer time-stamps must be the same for all epochs. Gaps are OK, duplicates are not.

Column names may be chosen freely (epoch and time index column names default to epoch_id, time).

Notes: The index column names default to epoch_id and time but any column may be designated as the epoch or time index, provided the conditions are met. Standard practice is to sequence the rows so time stamps are nested within epochs. Event-relative epochs are generally time-stamped so the event is at time=0 but this is not a fitgrid requirement.

Example: A canonical source of data epochs for fitgrid are multichannel “strip charts” as in EEG and MEG recordings. In this case, “epochs” are fixed-length segments extracted from the strip chart and time-stamped relative to an experimental event.

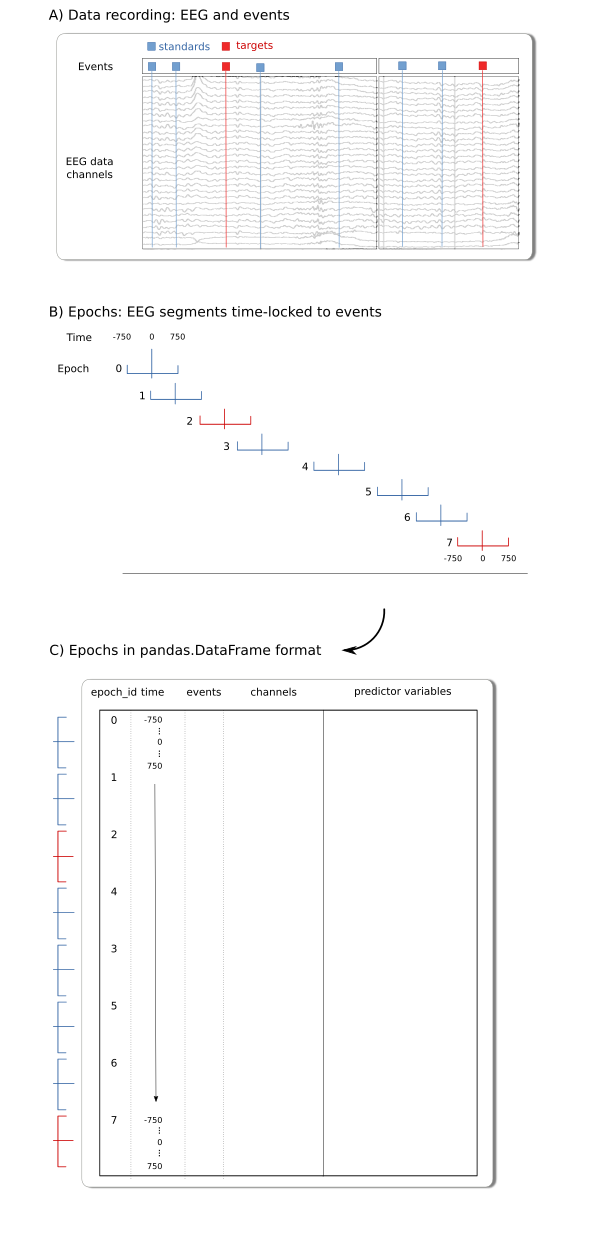
Data Ingestion ¶

Rows and columns epochs data can be loaded into a fitgrid.Epochs object from a pandas.DataFrame in memory or read from files in feather or HDF5 format.

For details on these data formats see pandas.read_feather and pandas.read_hdf).

Data Simulation.¶

fitgrid has a built-in function that generates data and creates Epochs data for testing.

Fitting a model¶

The following methods populate the FitGrid[time, channel] object. with statsmodels results for OLS model fits and lme4::lmer for linear mixed-effects fits.

Ordinary least squares: fitgrid.lm()

lm_grid = fitgrid.lm(
    epochs_fg,
    RHS='1 + categorical + continuous'
)

Linear mixed-effects: fitgrid.lmer()

lmer_grid = fitgrid.lmer(
    epochs_fg,
    RHS='1 + continuous + (continuous | categorical)'
)

User-defined (experimental): fitgrid.run_model()

The FitGrid[time, channel]¶

Slice by time, channel¶

Slice the FitGrid with pandas.DataFrame range : and label slicers. The range includes the upper bound.

lm_grid[:, ["MiCe", "MiPa"]]
lm_grid[-100:300, :]
lm_grid[0, "MiPa"]

Access results¶

Query the FitGrid results like a single fit object. Result grids are returned as as pandas.DataFrame or another FitGrid which can be queried the same way.

lmg_grid.params
lmg_grid.llf

Slice and access¶

lm_grid[-100:300, ["MiCe", "MiPa"].params

`LMFitGrid` methods¶

The fitted OLS grid provides time-series plots of selected model results: estimated coefficients fitgrid.lm.plot_betas() and adjusted \(R^2\) fitgrid.lm.plot_adj_rsquared() (see also fitgrid.utils() for additional model summary wrappers).

Saving and loading grids¶

Running models on large datasets can take a long time. fitgrid lets you save your grid to disk so you can restore them later without having to refit the models. However, saving and loading large grids may still be slow and generate very large files.

Suppose you run lmer like so:

grid = fitgrid.lmer(epochs, RHS='x + (x|a)')

Save the grid:

grid.save('lmer_results')

Later you can reload the grid:

grid = fitgrid.load_grid('lmer_results')

Warning

Fitted grids are saved and loaded with Python pickle which is not guaranteed to be portable across different versions of Python. Unpickling unknown files is not secure (for details see the Python docs). Only load grids you trust such as those you saved yourself. For reproducibility and portability fit the grid, collect the results you need, and export the dataframe to a standard data interchange format.

Model comparisons and summaries¶

To reduce memory demands when comparing sets of models, fitgrid provides a convenience wrapper, fitgrid.utils.summarize, that iteratively fits a list of models and collects a lightweight summary dataframe with key results for model interpretation and comparison. Unlike the primary FitGrid, the summary dataframe format is the same for fitgrid.lm and fitgrid.lmer. Some helper functions are available for visualizing selected summary results.

Model and data diagnostics (WIP)¶

Model and data diagnostics in the fitgrid framework is work in progress. For ordinary least squares fitting, there is some support for the native statsmodels OLS diagnostic measures. Diagostics that can be computed analytically from a single model fit, e.g., via the hat matrix diagonal, may be useable but many are not for realistically large data sets. The per-observation diagnostic measures, e.g., the influence of observations on estimated parameters, are the same size as the original data multiplied by the number of model parameters which may overload memory and measures that require on leave-one-observation-out model refitting take intractably long for large data sets. A minimal effort is made to guard the user from known trouble but the general policy is fitgrid stays out of the way so you can try what you want. If it works great, if it chokes, that’s the nature of the beast you are modeling.

Support for linear-mixed effects diagnostics in fitgrid is limited to a variance inflation factor computation implemented in Python as a proof-of-concept. fitgrid does not interface with mixed-effect model diagnostics libraries in R and plans are to improve support for mixed-effects modeling in Python rather than expand further into the R ecosystem.

fitgrid under the hood¶

How mixed effects models are run¶

Mixed effects models do not have a complete implementation in Python, so we interface with R from Python and use lme4 in R. The results that you get when fitting mixed effects models in fitgrid are the same as if you used lme4 directly, because we use lme4 (indirectly).

Multicore model fitting¶

On a multicore machine, it may be possible to significantly speed fitting by computing the models in parallel. fitgrid.lm uses statsmodels under the hood to fit a linear least squares model, which in turn employs numpy for calculations. numpy itself depends on linear algebra libraries that might be configured to use multiple threads by default. This means that on a 48 core machine, common linear algebra calculations might use 24 cores automatically, without any explicit parallelization. So when you explicitly parallelize your calculations using Python processes (say 4 of them), each process might start 24 threads. In this situation, 96 CPU bound threads are wrestling each other for time on the 48 core CPU. This is called oversubscription and results in slower computations.

To deal with this when running fitgrid.lm, we try to instruct the linear algebra libraries your numpy distribution depends on to only use a single thread in every computation. This then lets you control the number of CPU cores being used by setting the n_cores parameter in fitgrid.lm() and fitgrid.lmer().

If you are using your own 8-core laptop, you might want to use all cores, so set something like n_cores=7. On a shared machine, it’s a good idea to run on half or 3/4 of the cores if no one else is running heavy computations.

Note that fitgrid parallel processing counts the “logical” cores available to the operating system and this may differ from the number of physical cores, depending on the system hardware and setting, e.g., Intel CPUs with hyperthreading enabled. The Python package psutil and psutil.cpu_count(logical=True) and psutil.cpu_count(logical=False) may be useful for interrogating the system about the available resources.